【量化金融】行业中常见的面试问题-答案

题目请关注

解答

题目1

分成两种情况：

  • n为偶：$n^n=(n^{(n/2)})^2$，n/2为整数，成立。[100:400]的任意偶数成立，一共有$(400-100)/2+1=151个。
  • n为奇：此时$n^n$为完全平方的条件是n为完全平方，因为$n^n = (x^2)^n = (x^n)^2$（设$n=x^2$）。所以$100<n<400$ —> $10^2<x^2<20^2$ —> $10<x<20$ ，满足的奇数有11、13、15、17、19。

所以一共有151+5=156个。

题目2

最短的两条边合成一条边（3+2=5）与最长的边（12）组成矩形，最短路径就是矩形的对角线$\sqrt{(5^2+12^2})$=13

题目3

将题目描述情况当作一个事件，此事件发生概率为0.5*0.5=0.25，因此预期次数为1/0.25=4

题目4

经典条件概率题目，两个小孩，一共4种可能，“男男”，“男女”，“女男”，“女女”，概率均为0.25。

  1. P(另一个是女孩|其中一个是女孩) = P(女女) / P(男女 or 女男 or 女女)=0.25/0.75=1/3

  2. P(另一个是女孩|先出生的一个是女孩) = P(女女) / P(女男 or 女女)=0.25/0.5=0.5

  3. P(另一个是女孩|有一个女儿叫维多利亚) = P(女女) / P(男女 or 女男 or 女女)=0.25/0.75=1/3

题目5

Brouwer fixed-point theorem（布劳威尔不动点定理）

设*f(x)*是定义在集合X⊂R^n上的实函数，且f(x)∈X,∀x∈X。

  1. 如果f(x)是连续的；
  2. 且X为一非空的有界凸闭集(非空紧凸集)；
  3. 则至少存在一个x*∈X使f(x*)=x*。即f(x)至少存在一个不动点。

定义一个函数*f(x)，x为水分子在煮开前的某一刻的位置，f(x)*为水分子在煮开后的某一刻的位置。

对于条件1，题目中已经给出水分子在煮沸过程中的位置改变是连续的，对应函数关系f(x)是连续的

对于条件2，题目已给出锅子是封闭的，满足非空紧凸集的拓扑定义：一定有完全边界且任何存在极限的X包含的元素序列的极限点属于X。

因此，符合不动点定理的结论，在一锅水分子X中，至少存在一个水分子x*∈X，使得f(x*)=x*。即至少有一个水分子自始至终都处在原位。

题目6

kNVkwFzRuwPA8GWbH4G_4Q

4AB_D4r2l2fhxlhuhObIMA

题目7

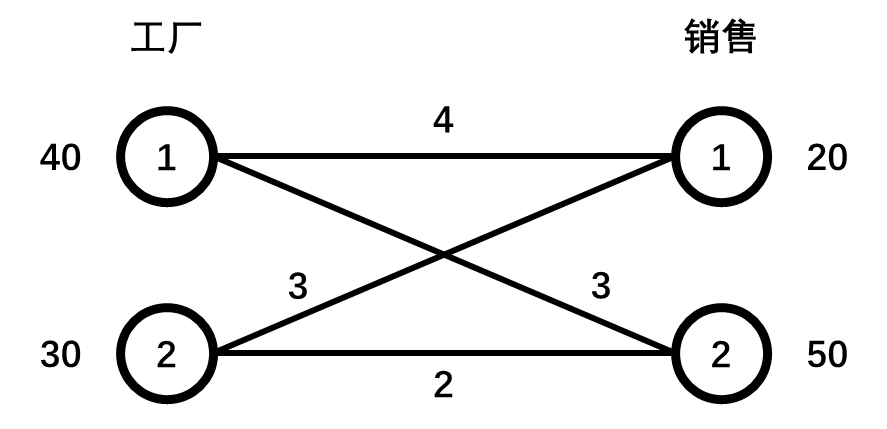
image-20230713172531102

设:
$$
1–x->1; \ \ 1–y->2; \
2–z->1; \ \ 2–w->1 \
$$
可得最优化函数组：
$$
min. 4x+3y+3z+2w \
s.t.\left{
\begin{aligned}
\ \ x+y=40 \ \ \ \ \ \ \ \
\ \ z+w=30 \ \ \ \ \ \ \ \
\ \ x+z=20 \ \ \ \ \ \ \ \
\ \ y+w=50 \ \ \ \ \ \ \ \
\end{aligned}
\right.
$$
事实上我们发现，$4x+3y+3z+2w = 3(x+y)+(x+z)+2(z+w)=200$

如果将工厂1运送至销售点1的价格提高至5，这个式子5x+3y+3z+2w就有了解：

$min(5x+3y+3z+2w) = min(x+200)$

所以x=0；y=40；z=20；w=10

题目8

ZXEdyuH3QoUGikqaGXTlrQ

最后一问可以使用代码来解决：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import random

import math

import numpy as np

import matplotlib.pyplot as plt

def random_walk(n):
    x, y = 0, 0
    for _ in range(n):
        direction = random.choice(["上", "下", "左", "右"])
        if direction == "上":
            y += 1
        elif direction == "下":
            y -= 1
        elif direction == "左":
            x -= 1
        elif direction == "右":
            x += 1
    return x, y

def calculate_distance(n, num_simulations):
    total_distance = 0
    for _ in range(num_simulations):
        x, y = random_walk(n)
        distance = math.sqrt(x ** 2 + y ** 2)
        total_distance += distance
    return total_distance / num_simulations

num_simulations = 10000
step_range = range(1, 51)  # 计算1到50步的平均距离
average_distances = [calculate_distance(n, num_simulations) for n in step_range]

plt.plot(step_range, average_distances, marker='o')
plt.xlabel("步数 (n)")
plt.ylabel("与原点的平均距离")
plt.title("醉汉游走：步数与平均距离的关系")
plt.grid(True)
plt.show()

题目9

用C_n^k代表组合数也就是\frac_{(n-k)!k!}^{n!}，n!=123…*n

  1. $C_n^kp^k(1-p)^{(n-k)}$

  2. $1-(1-p)^n$

  3. 掷硬币抛掷为独立事件，因此之前的抛掷情况不影响之后投掷结果的概率，因此答案是p。也可以用贝叶斯公式算一下。

题目10

算是最简单的动态规划问题了，甚至没有故事背景，直接解决：

1
2
3
4
5
6
7
8
9
10
11
def min_path(n, grid):
    dp = [[0]*n for _ in range(n)]
    dp[0][0] = grid[0][0]
    for i in range(1, n):
        dp[i][0] = dp[i-1][0] + grid[i][0]
    for j in range(1, n):
        dp[0][j] = dp[0][j-1] + grid[0][j]
    for i in range(1, n):
        for j in range(1, n):
            dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])
    return dp[-1][-1]
1
2
3
4
5
6
7
8
9
最终dp：
dp = [
  [1 , 4 , 5, 10],
  [2 , 7 , 6, 10],
  [6 , 8 , 7, 13],
  [13, 11, 9, 16]
]

因此，结果为16