【量化金融】三因子模型策略实现

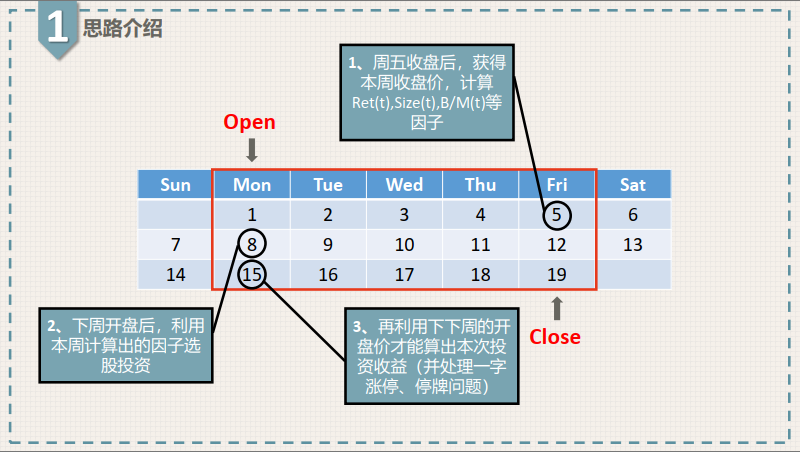
策略简介

利用Fama三因子模型构建的A股周度百股策略。

clsl

环境与数据准备

1
2
3
4
5
6
7
8
9
import numpy as np
from tqdm import tqdm
import pandas as pd
import os
import gc
import warnings
warnings.filterwarnings('ignore')

from quantools import backtest
1
2
3
4
5
6
7
8
9
10
11
stk_data = pd.read_csv("../data/stk_data.csv")
stk_data['close_date'] = pd.to_datetime(stk_data['close_date'])
stk_data['open_date'] = pd.to_datetime(stk_data['open_date'])

open_days_data = pd.read_csv("../data/open_days_data.csv")
open_days_data['date'] = pd.to_datetime(open_days_data['date'])

equity = pd.read_csv("../data/eqy_belongto_parcomsh.csv")
equity['rpt_date'] = pd.to_datetime(equity['rpt_date'])

os.mkdir("../cal_data") # 存储计算结果的路径
1
2
3
4
5
6
7
8
9
10
11
# 沪深两市股票20060101-20230928周度股票数据 
# stock_code:股票代码
# open_date:开盘时间
# close_date:收盘时间
# open:后复权开盘价
# close:后复权收盘价
# uadj_close:未复权收盘价
# total_shares:总股本数

print(stk_data.shape)
stk_data.head()
TOTAL_SHARES CLOSE OPEN stock_code open_date close_date uadj_close
0 1.945822e+09 160.348451 153.344151 000001.SZ 2006-01-04 2006-01-06 6.41
1 1.945822e+09 155.345379 160.098298 000001.SZ 2006-01-09 2006-01-13 6.21
2 1.945822e+09 155.845687 154.594919 000001.SZ 2006-01-16 2006-01-20 6.23
3 1.945822e+09 158.847530 155.845687 000001.SZ 2006-01-23 2006-01-25 6.35
4 1.945822e+09 155.345379 158.847530 000001.SZ 2006-02-06 2006-02-10 6.21 
1
2
3
4
5
6
# 沪深两市上市公司20050930-20230630报告期内归属母公司的股东权益数据 
# stock_code:股票代码
# rpt_date:报告期日期
# eqy_belongto_parcomsh:归属母公司的股东权益
print(equity.shape)
equity.head()
stock_code EQY_BELONGTO_PARCOMSH rpt_date
0 000001.SZ 5.014966e+09 2005-09-30
1 000002.SZ 6.738774e+09 2005-09-30
2 000004.SZ 8.952654e+07 2005-09-30
3 000005.SZ 8.290555e+08 2005-09-30
4 000006.SZ 1.007023e+09 2005-09-30 
1
2
3
4
5
6
7
8
9
10
11
# 沪深两市股票20060101-20230928，每周开盘日的高开低收量
# stock_code:股票代码
# date:交易日期
# high:最高价
# open:开盘价
# low:最低价
# close:收盘价
# volume:交易量

print(open_days_data.shape)
open_days_data.head()
stock_code HIGH OPEN LOW CLOSE VOLUME date
0 000001.SZ 158.347222 153.344151 153.093997 157.096455 15445068.0 2006-01-04
1 000002.SZ 206.631220 194.684662 194.684662 206.188755 38931043.0 2006-01-04
2 000004.SZ 13.191923 13.035620 12.941839 13.098141 401500.0 2006-01-04
3 000005.SZ 9.436105 9.155268 9.042934 9.379937 3713641.0 2006-01-04
4 000006.SZ 18.698245 18.698245 18.698245 18.698245 0.0 2006-01-04

数据计算

计算三因子

在这一步，考虑到公司财报的报告期各不相同，因此采用每批次财报的截止日期作为数据更新日期，也就是说计算账面市值比等因子时，计算因子的日期与财报日期的对应关系如下：

因子日期 报告期
5、6、7、8月 一季报（最晚04.30公布）
9、10月 半年报（最晚08.30公布）
11、12月 三季报（最晚10.30公布）
1、2、3、4月 去年三季报（最晚去年10.30公布）

其中，由于年报与一季报截止时间一致，而一季报比去年年报数据更新，因此我们不使用年报数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 计算市值
stk_data['mkt_cap'] = stk_data['TOTAL_SHARES'] * stk_data['uadj_close']

# 计算每个交易周对应的报告期（用于匹配所有者权益）
def match_rpt_date(date):
    """
        将日期转化为对应的报告期；
        基于：一季报最晚4/30公布，半年报8/30，三季报10/30，年报来年4/30（因此不用）
    """
    y = date.year
    m = date.month
    if m in (5, 6, 7, 8): return f"{y}0331"
    elif m in (9, 10): return f"{y}0630"
    elif m in (11, 12): return f"{y}0930"
    elif m in (1, 2, 3, 4): return f"{y-1}0930"

stk_data['rpt_date'] = pd.to_datetime(stk_data['close_date'].apply(lambda x: match_rpt_date(x)))
1
all_data = pd.merge(stk_data, equity, on=['stock_code', 'rpt_date'], how='left')
1
2
3
odd = {}
for key in tqdm(['HIGH', 'OPEN', 'LOW', 'CLOSE', 'VOLUME']):
    odd[key] = pd.pivot(open_days_data, index='date', columns='stock_code', values=key)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
odd['pred_rtn'] = (odd['OPEN'].shift(-2)-odd['OPEN'].shift(-1))/odd['OPEN'].shift(-1)

pred_rtn_na = odd['pred_rtn'].isna() # 不要把空值变成0

# 下周停牌的股票只能获得0的收益
vol0 = odd['VOLUME'].shift(-1)==0 
volna = odd['VOLUME'].shift(-1).isna()
odd['pred_rtn'][vol0 | volna & (~pred_rtn_na)] = 0 

# 下周一字涨停的股票无法买入，只能获得0的收益
yz = odd['HIGH'].shift(-1)==odd['LOW'].shift(-1) # “一字”，价格没有变化
zt = ~(odd['CLOSE'].shift(-1) <= odd['CLOSE']) # “涨停”，价格不比上周高
odd['pred_rtn'][yz & zt & (~pred_rtn_na)] = 0 

pred_rtn = odd['pred_rtn'].stack().reset_index().rename(columns={0: 'pred_rtn', 'date': 'open_date'})

all_data = pd.merge(all_data, pred_rtn, on=['open_date', 'stock_code'], how='left')
all_data = all_data[~all_data['pred_rtn'].isna()]

del odd
gc.collect() # 释放内存
1
2
3
4
5
6
7
8
9
10
11
# 计算周收益率因子
close = pd.pivot(all_data, index='close_date', columns='stock_code', values='CLOSE')
fac_ret = (close-close.shift(1))/close.shift(1)
fac_ret = fac_ret.stack().reset_index().rename(columns={0: 'fac_ret', 'date': 'close_date'})
all_data = pd.merge(all_data, fac_ret, on=['close_date', 'stock_code'], how='left')

# 计算规模因子
all_data['fac_size'] = np.log(all_data['mkt_cap']/1000000)

# 账面市值比因子
all_data['fac_bm'] = all_data['EQY_BELONGTO_PARCOMSH'] / all_data['mkt_cap']
1
2
3
factors = all_data[['stock_code', 'close_date', 'pred_rtn', 'fac_ret', 'fac_size', 'fac_bm']].reset_index(drop=True)
factors = factors[~factors['pred_rtn'].isna()]
factors.head()
stock_code close_date pred_rtn fac_ret fac_size fac_bm
0 000001.SZ 2006-01-06 -0.034375 NaN 9.431299 0.402075
1 000001.SZ 2006-01-13 0.008091 -0.031201 9.399601 0.415024
2 000001.SZ 2006-01-20 0.019262 0.003221 9.402816 0.413692
3 000001.SZ 2006-01-25 -0.022047 0.019262 9.421895 0.405874
4 000001.SZ 2006-02-10 0.004831 -0.022047 9.399601 0.415024 
1
factors.to_csv("../cal_data/factors.csv", index=False)

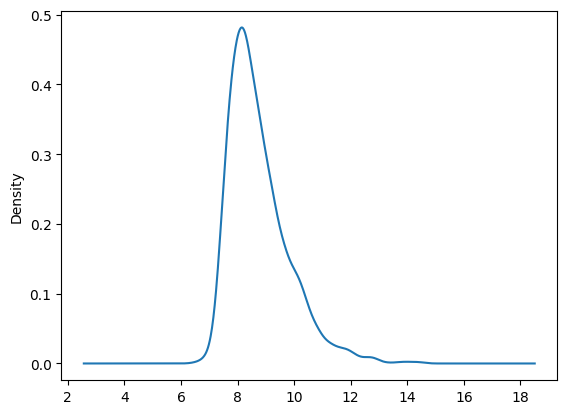
因子截尾处理

1
2
3
# 截尾前(没有偏好，随便选的)
fac_name = 'fac_size'
factors[factors['close_date']=='2019-10-18'][fac_name].plot.kde(title="2019-10-18日 Size因子分布情况（截尾前）")

0_三因子模型策略实现_18_1

1
2
3
factors = backtest.winsorize_factor(factors, 'fac_size')
factors = backtest.winsorize_factor(factors, 'fac_ret')
factors = backtest.winsorize_factor(factors, 'fac_bm')
1
2
# 截尾后
factors[factors['close_date']=='2019-10-18'][fac_name].plot.kde(title="2019-10-18日 Size因子分布情况（截尾后）")

0_三因子模型策略实现_20_1
​

对单个因子测试

通过Fama-MacBeth回归验证模型效果

1
2
3
4
5
res_list = []
for fac_name in ['fac_size', 'fac_ret', 'fac_bm']:
    res_list.append(backtest.fama_macbeth(factors, fac_name))
fama_macbeth_res = pd.DataFrame(res_list)
fama_macbeth_res
fac_name t p pos_count neg_count
0 fac_size -4.576268 5.395101e-06 362 541
1 fac_ret -10.642792 5.330462e-25 290 612
2 fac_bm 4.019551 6.317205e-05 464 439
针对这一分析结果，三个因子t检验显著区别于0，是比较有效的因子；而其中账面市值比显著为正，其他两个显著为负数，也符合日常学术研究中对其的认知。

其中，账面市值比因子回归后斜率分别为正负的数量基本相同，区分效应较差，因此从这一维度来说，他的效果并不是很好。

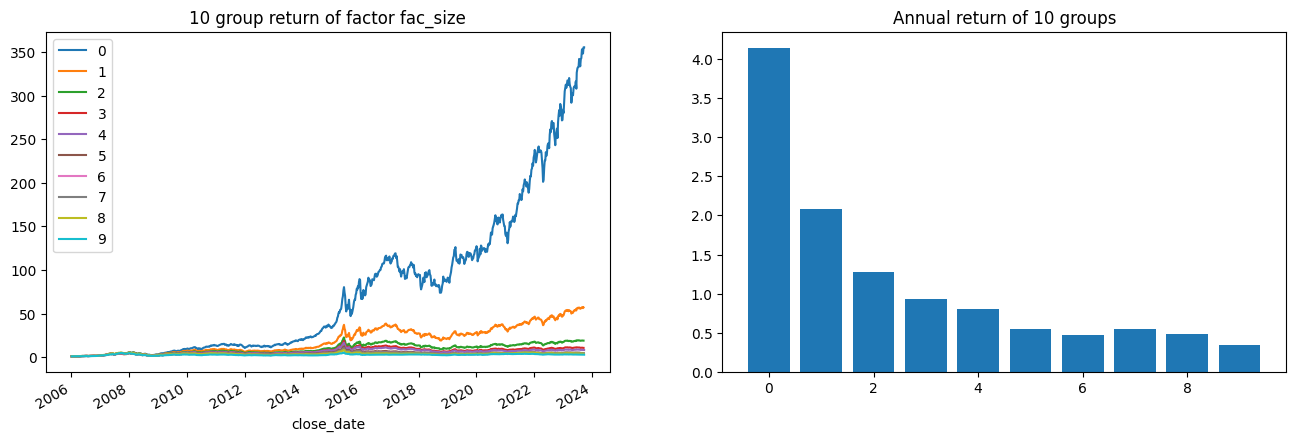
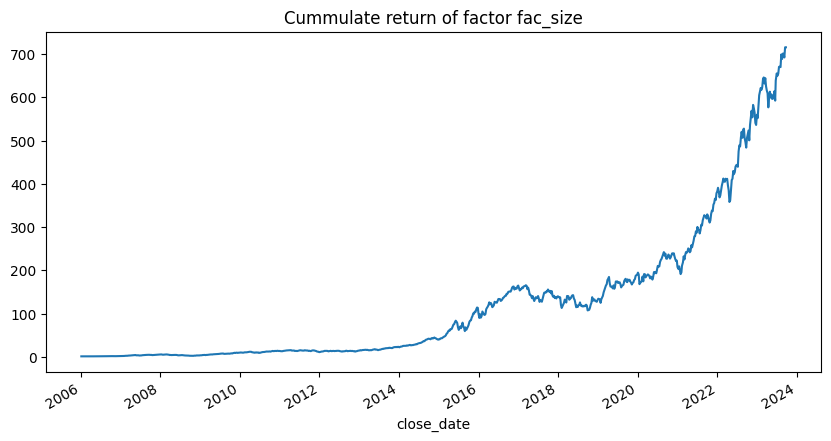
单因子分组收益情况

1
group_rtns, group_cum_rtns = backtest.group_return_analysis(factors, 'fac_size')

0_三因子模型策略实现_26_1

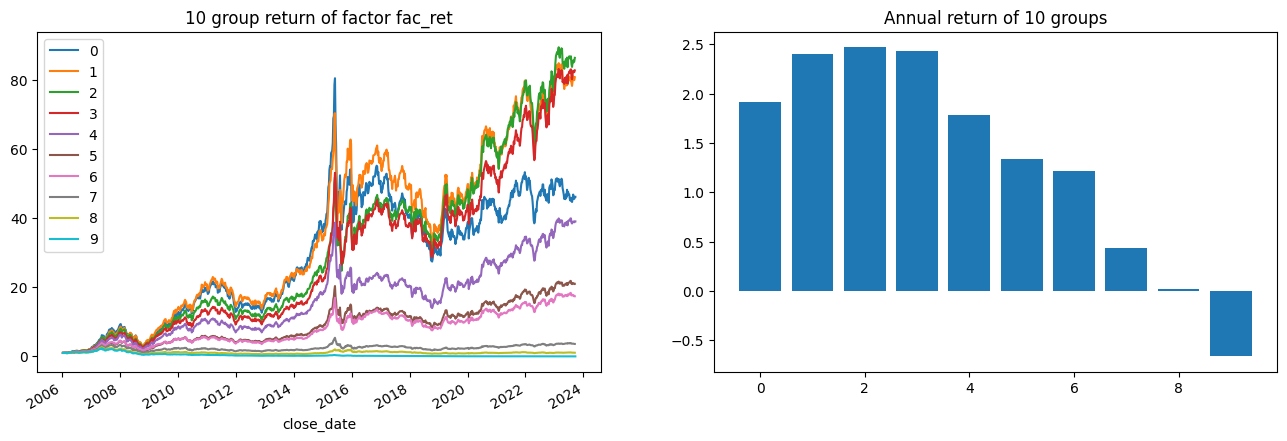
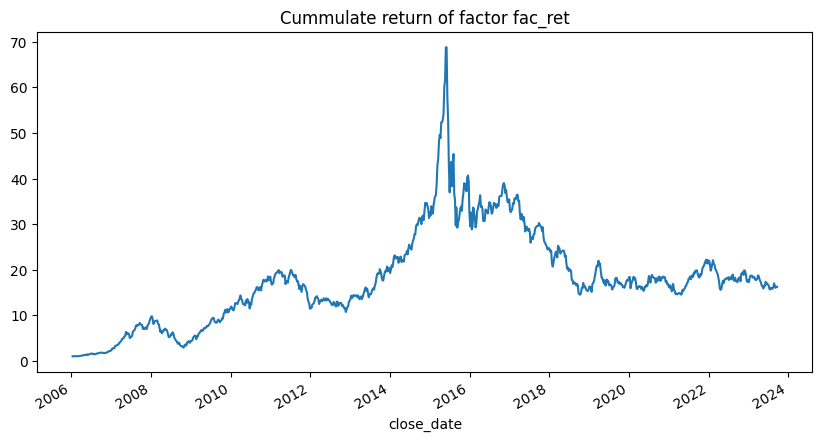
1
group_rtns, group_cum_rtns = backtest.group_return_analysis(factors, 'fac_ret')

0_三因子模型策略实现_27_1

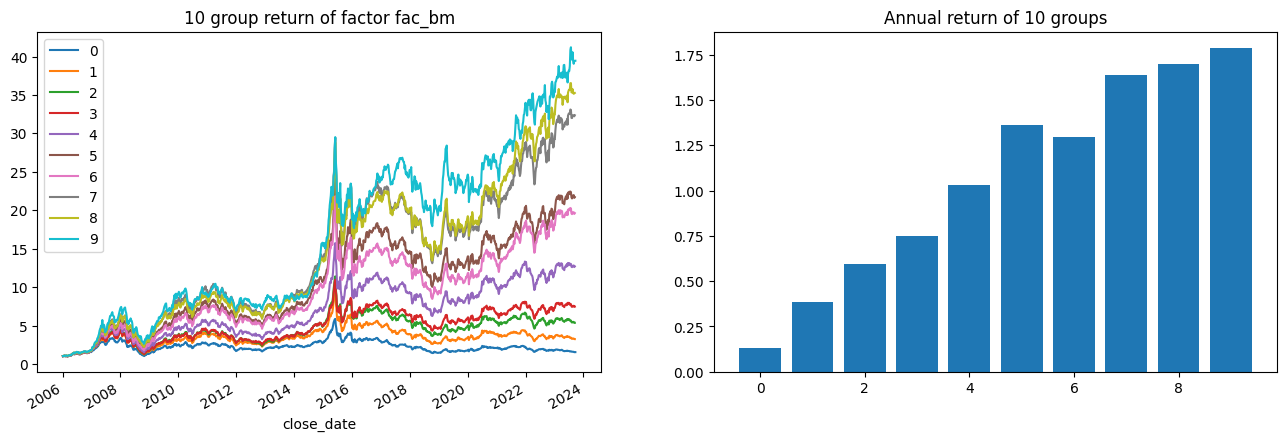
1
group_rtns, group_cum_rtns = backtest.group_return_analysis(factors, 'fac_bm')

0_三因子模型策略实现_28_1

回测后看出，三个因子都有一定的分组效果，其中账面市值比与市值因子分组效果最好，收益率因子分组效果相对差一些。

单因子周度百股策略回测

1
2
rtn, evaluate_result = backtest.backtest_1week_nstock(factors, 'fac_ret', True)
evaluate_result
sharpe_ratio max_drawdown max_drawdown_start max_drawdown_end sortino_ratio annual_return annual_volatility section
0 1.405346 0.789046 2015-06-05 2018-10-12 2.030548 1.178091 0.763147 Sum
1 6.653799 0.108753 2006-06-30 2006-07-28 9.882821 67.674182 0.674358 2006
2 7.957098 0.217392 2007-05-18 2007-06-22 11.966749 1336.033077 0.975551 2007
3 -2.535012 0.699955 2008-01-11 2008-10-24 -4.945847 -0.975181 1.181429 2008
4 6.570332 0.143081 2009-02-06 2009-02-20 8.999942 121.088407 0.783940 2009
5 3.688373 0.198535 2010-04-02 2010-06-25 6.296923 9.382755 0.702845 2010
6 -3.329041 0.426803 2011-07-08 2011-12-30 -4.826786 -0.906297 0.645434 2011
7 1.483952 0.243869 2012-03-02 2012-11-23 2.545457 1.049363 0.604799 2012
8 4.117017 0.134629 2013-05-24 2013-06-21 7.282607 7.479792 0.558735 2013
9 4.479553 0.096290 2014-11-21 2014-12-26 9.303073 8.344907 0.531904 2014
10 0.683548 0.575212 2015-06-05 2015-09-11 0.882963 -0.014136 1.347235 2015
11 0.957265 0.155600 2016-04-08 2016-05-06 1.431324 0.558164 0.753643 2016
12 -3.226729 0.330036 2017-03-17 2017-12-22 -4.293738 -0.829643 0.506809 2017
13 -2.996387 0.425417 2018-03-23 2018-10-12 -4.204086 -0.896640 0.677827 2018
14 1.305734 0.287685 2019-03-29 2019-08-02 2.413080 0.887732 0.639300 2019
15 -0.294687 0.168351 2020-02-14 2020-05-15 -0.414377 -0.325593 0.640734 2020
16 2.825869 0.139483 2021-02-10 2021-04-23 5.050823 2.591822 0.496437 2021
17 -1.196824 0.294684 2022-02-11 2022-04-22 -2.205050 -0.610259 0.625781 2022
18 -1.182782 0.165736 2023-03-31 2023-07-21 -2.770508 -0.440561 0.418921 2023
6 -3.329041 0.426803 2011-07-08 2011-12-30 -4.826786 -0.906297 0.645434 2011
7 1.483952 0.243869 2012-03-02 2012-11-23 2.545457 1.049363 0.604799 2012
8 4.117017 0.134629 2013-05-24 2013-06-21 7.282607 7.479792 0.558735 2013
9 4.479553 0.096290 2014-11-21 2014-12-26 9.303073 8.344907 0.531904 2014
10 0.683548 0.575212 2015-06-05 2015-09-11 0.882963 -0.014136 1.347235 2015
11 0.957265 0.155600 2016-04-08 2016-05-06 1.431324 0.558164 0.753643 2016
12 -3.226729 0.330036 2017-03-17 2017-12-22 -4.293738 -0.829643 0.506809 2017
13 -2.996387 0.425417 2018-03-23 2018-10-12 -4.204086 -0.896640 0.677827 2018
14 1.305734 0.287685 2019-03-29 2019-08-02 2.413080 0.887732 0.639300 2019
15 -0.294687 0.168351 2020-02-14 2020-05-15 -0.414377 -0.325593 0.640734 2020
16 2.825869 0.139483 2021-02-10 2021-04-23 5.050823 2.591822 0.496437 2021
17 -1.196824 0.294684 2022-02-11 2022-04-22 -2.205050 -0.610259 0.625781 2022
18 -1.182782 0.165736 2023-03-31 2023-07-21 -2.770508 -0.440561 0.418921 2023

0_三因子模型策略实现_31_1

1
2
rtn, evaluate_result = backtest.backtest_1week_nstock(factors, 'fac_size', True)
evaluate_result
sharpe_ratio max_drawdown max_drawdown_start max_drawdown_end sortino_ratio annual_return annual_volatility section
0 3.122859 0.610775 2008-01-11 2008-10-24 4.453695 5.248983 0.658517 Sum
1 3.780915 0.082394 2006-09-29 2006-11-10 6.824324 7.448274 0.615477 2006
2 7.619150 0.277240 2007-05-18 2007-06-22 7.588304 550.342103 0.891182 2007
3 -1.678621 0.610775 2008-01-11 2008-10-24 -2.910806 -0.884322 0.992800 2008
4 7.547957 0.115055 2009-02-06 2009-02-20 10.933357 167.053901 0.719293 2009
5 3.022128 0.245051 2010-04-02 2010-06-25 4.223931 4.525651 0.633368 2010
6 -1.694132 0.302932 2011-04-15 2011-12-30 -2.558479 -0.681412 0.576306 2011
7 2.662808 0.146320 2012-03-02 2012-11-23 4.112191 3.122259 0.600360 2012
8 5.374411 0.131401 2013-05-24 2013-06-21 8.249390 9.844832 0.465409 2013
9 7.121590 0.112333 2014-11-21 2014-12-26 13.799625 13.415354 0.386941 2014
10 5.110443 0.288560 2015-06-05 2015-08-28 6.782858 81.649740 0.961526 2015
11 4.188296 0.088634 2016-04-08 2016-05-06 5.508037 11.105522 0.647160 2016
12 -1.330087 0.232662 2017-03-10 2017-07-14 -2.252187 -0.552614 0.507959 2017
13 -0.081387 0.247255 2018-05-18 2018-09-28 -0.119885 -0.276922 0.731677 2018
14 3.747108 0.148059 2019-04-12 2019-05-31 5.904712 5.290640 0.529220 2019
15 1.042077 0.141963 2020-08-28 2020-12-31 1.448336 0.533958 0.560545 2020
16 6.727338 0.085806 2021-01-15 2021-01-29 16.085113 18.249285 0.457282 2021
17 3.816535 0.131406 2022-02-25 2022-04-22 8.065974 5.825747 0.542672 2022
18 4.185553 0.107099 2023-03-03 2023-04-14 8.362568 4.334733 0.421798 2023

0_三因子模型策略实现_32_1

1
2
rtn, evaluate_result = backtest.backtest_1week_nstock(factors, 'fac_bm')
evaluate_result
sharpe_ratio max_drawdown max_drawdown_start max_drawdown_end sortino_ratio annual_return annual_volatility section
0 2.006960 0.638422 2008-01-11 2008-10-24 2.918252 1.847405 0.617145 Sum
1 5.618410 0.105872 2006-06-30 2006-08-11 9.420005 21.852138 0.590378 2006
2 7.354710 0.281662 2007-05-18 2007-06-22 8.206541 980.089048 1.019448 2007
3 -2.479428 0.638422 2008-01-11 2008-10-24 -4.484640 -0.960315 1.067600 2008
4 6.410670 0.142736 2009-02-06 2009-02-20 10.016987 131.546624 0.820762 2009
5 0.156546 0.274959 2010-04-02 2010-06-25 0.242633 -0.062901 0.555388 2010
6 -2.983162 0.329127 2011-04-15 2011-12-30 -5.263885 -0.730526 0.410657 2011
7 2.215259 0.162853 2012-02-24 2012-09-14 4.250416 1.304317 0.415575 2012
![0_三因子模型策略实现_33_1](/0_三因子模型策略实现_33_1.png)

多因子组合

简单分组打分法

1
2
rtn, evaluate_result = backtest.mutifactor_score(factors, ['-fac_ret', '-fac_size', 'fac_bm'], group_num=10)
evaluate_result
sharpe_ratio max_drawdown max_drawdown_start max_drawdown_end sortino_ratio annual_return annual_volatility section
0 2.762777 0.606990 2008-02-29 2008-10-24 3.828052 4.585105 0.718640 Sum
1 5.532422 0.102080 2006-06-30 2006-08-11 10.268628 26.228477 0.636676 2006
2 8.101543 0.287660 2007-05-18 2007-06-22 8.857011 2223.268814 1.031276 2007
3 -0.937202 0.606990 2008-02-29 2008-10-24 -1.643112 -0.829617 1.169914 2008
4 7.927451 0.138606 2009-02-06 2009-02-20 11.627565 466.483920 0.826747 2009
5 4.065468 0.241853 2010-04-02 2010-06-25 5.996514 11.165462 0.672587 2010
6 -2.182011 0.333801 2011-03-18 2011-12-30 -3.358018 -0.776748 0.602593 2011
7 2.119900 0.196653 2012-03-02 2012-11-23 3.458198 1.997337 0.603504 2012
8 4.936706 0.168503 2013-05-24 2013-06-21 7.691246 9.718052 0.508523 2013
9 5.649539 0.083951 2014-11-21 2014-12-26 11.179287 9.436769 0.433277 2014
10 2.837548 0.410130 2015-06-05 2015-07-03 3.294351 12.990229 1.190048 2015
11 3.568117 0.091504 2016-04-08 2016-05-06 4.329537 7.026963 0.643478 2016
12 -1.778931 0.230229 2017-02-17 2017-12-15 -2.780930 -0.592425 0.447876 2017
13 -0.659488 0.275744 2018-01-19 2018-10-12 -0.949217 -0.497481 0.686670 2018
14 2.215944 0.231712 2019-04-12 2019-08-02 4.274694 2.091116 0.585855 2019
15 1.242012 0.138234 2020-01-03 2020-01-17 1.719817 0.735576 0.577622 2020
16 5.216823 0.104639 2021-09-03 2021-10-22 10.806690 7.976897 0.440638 2021
17 1.588294 0.164306 2022-02-25 2022-04-22 3.120165 1.013708 0.526335 2022
18 3.335436 0.104342 2023-02-24 2023-05-19 6.708995 2.018183 0.349659 2023

0_三因子模型策略实现_36_1

相比于单个”市值“因子，因子组合后效果变差了。

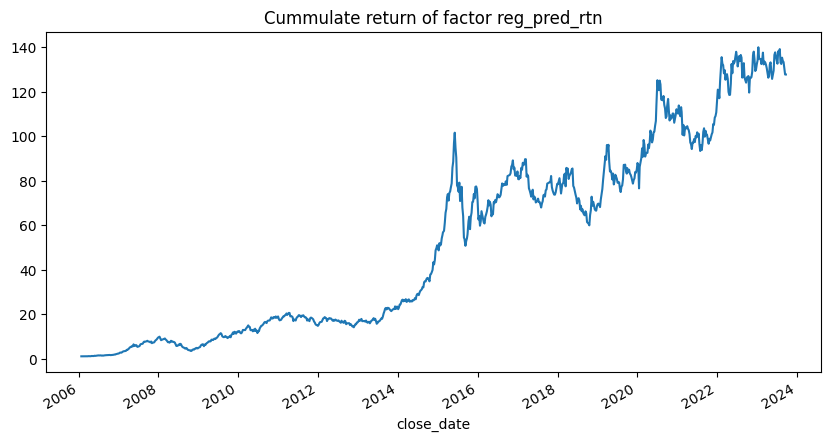
多元回归选股法

1
rtn, evaluate_result = backtest.mutifactor_regression(factors, ['fac_ret', 'fac_size', 'fac_bm'], stock_num=100, plot=True)

0_三因子模型策略实现_39_1

1
evaluate_result
sharpe_ratio max_drawdown max_drawdown_start max_drawdown_end sortino_ratio annual_return annual_volatility section
0 2.381925 0.653284 2008-01-11 2008-10-24 3.633037 2.883003 0.663260 Sum
1 7.397497 0.083543 2006-07-21 2006-08-11 14.551758 80.247146 0.625025 2006
2 8.605610 0.176219 2007-05-18 2007-06-22 12.445344 1427.010829 0.901967 2007
3 -2.899683 0.653284 2008-01-11 2008-10-24 -5.515209 -0.960043 0.949763 2008
4 5.760640 0.194681 2009-07-24 2009-09-25 10.102339 88.968733 0.848765 2009
5 3.671218 0.230784 2010-04-02 2010-06-25 5.466090 8.329292 0.671275 2010
6 -2.037976 0.284170 2011-04-08 2011-12-30 -3.026109 -0.713988 0.541419 2011
7 1.235993 0.245804 2012-03-02 2012-11-23 2.141001 0.664276 0.520239 2012
8 3.641103 0.138178 2013-05-24 2013-06-21 6.342497 4.966395 0.530263 2013
9 7.529679 0.045554 2014-03-14 2014-03-21 17.314748 37.479723 0.504501 2014
10 2.234365 0.500596 2015-06-05 2015-09-11 3.162736 4.403217 0.969233 2015
11 1.734332 0.101322 2016-04-08 2016-05-06 2.097476 1.306984 0.579563 2016
12 -0.528623 0.242558 2017-03-10 2017-08-04 -0.667913 -0.286437 0.448402 2017
13 -0.812079 0.301313 2018-03-23 2018-10-19 -1.385928 -0.489442 0.606122 2018
14 2.260950 0.221067 2019-04-12 2019-08-02 4.214248 1.881747 0.529546 2019
15 2.290055 0.152632 2020-07-03 2020-12-04 3.748461 2.656131 0.660382 2020
16 0.660965 0.179802 2021-01-15 2021-07-30 0.985279 0.216939 0.447280 2021
17 1.549873 0.132950 2022-06-24 2022-10-21 2.930357 0.977742 0.528017 2022
18 -0.475897 0.101506 2023-01-13 2023-05-19 -0.929460 -0.216187 0.371352 2023
对比前面的诸多策略，该策略的收益率并不算高（尤其和市值因子相比），这也是因为我们回归后的系数滞后了两周才进行预测的结果。

但是，整体来看该策略的效果是比Ret,B/M因子的效果好的，而且相比于Size因子，该策略可以很好的消除市场风格的影响。

在2017年的大盘股行情中，该策略的最大回撤只有25%，比单纯的Size因子好很多。